

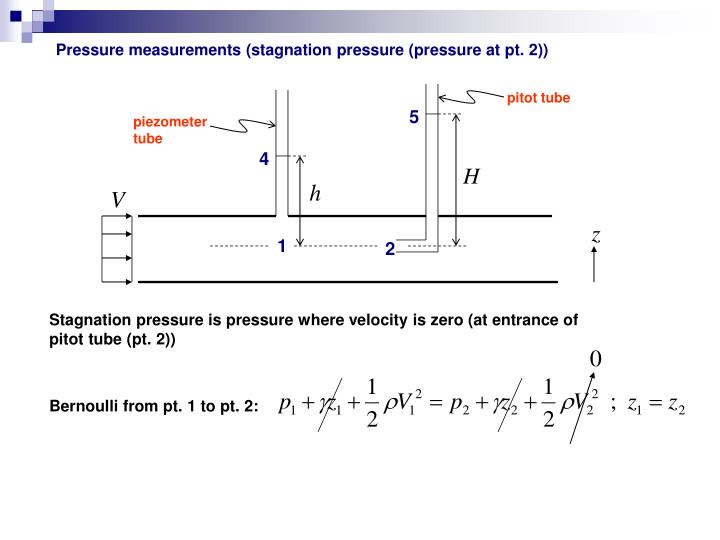
Therefore, the Bernoulli equation states that the total pressure along a streamline is constant. The sum of the static, dynamic, and hydrostatic pressures is called the total pressure. ρgz is the hydrostatic pressure, which is not pressure in a real sense since its value depends on the reference level selected it accounts for the elevation effects, i.e., of fluid weight on pressure.ρv 2/2 is the dynamic pressure it represents the pressure rise when the fluid in motion is brought to a stop isentropically.This is the same as the pressure used in thermodynamics property tables. P is the static pressure (it does not incorporate any dynamic effects) it represents the actual thermodynamic pressure of the fluid.This phenomenon can be made more visible by multiplying the Bernoulli equation by the density ρ:Įach term in this equation has pressure units, and thus each term represents some kind of pressure: Therefore, the kinetic and potential energies of the fluid can be converted to flow energy (and vice versa) during flow, causing the pressure to change. The Bernoulli equation states that the sum of the flow, kinetic, and potential energies of a fluid particle along a streamline is constant. The stagnation pressure is the sum of static and dynamic pressures, as given by Eq2 below. Static, Dynamic, and Stagnation Pressures Includes over 250 problems with complete detailed solutions.EngArc - L - Static, Dynamic, and Stagnation Pressures Practice Homework and Test problems now available in the 'Eng Fluids' mobile app For example, theĮGL and HGL for frictionless flow in a duct are shown in the figure. Height a fluid column would rise in a piezometer. Sometimes, this is also referred as the piezometric head and is the On the other hand, the HGL is the sum of static pressure The EGL is a constant for frictionless flow where no work or heat isĪssociated with the process. The total head available with respect to a chosen datum (i.e., a reference Graphical interpretation of Bernoulli's equation. Where p 1 and p 2 are known from the height of the fluid column in the piezometer and Pitot tube, respectively.Įnergy grade line (EGL) and the hydraulic grade line (HGL) provide a Since V 2 = 0, the velocity at point 1 is Providing the stagnation pressure measurement.Īpplying Bernoulli's equation between points 1 and 2 as shown in the figure, and canceling the elevations (equal values) gives, By perfectly aligning the Pitot tube with theįlow, the flow will come to a stop at the tip of the Pitot tube, hence Stagnation pressure is the pressure when the flow has a stagnation The Pitot tube, as shown in the figure, can be used to measure the stagnation

Static pressureĬan be measured using a piezometer. The assumptions made in deriving Bernoulli's equation are:Ī combination of piezometer and pitot tubeĬan be used to obtain the velocity at a specific point. To some restrictions, and can only be applied to certain flow situations. However, one should realize that Bernoulli's equation is subject Applying Bernoulli's equation between points 1 and 2 as shown in the figures yields, It can be applied to solve simple problems, such as flow from a tank (free jets), flow under a sluice gate and flow through a nozzle. Where p is the static pressure, ρV 2/2 is the dynamic pressure, and ρgz isīernoulli's equation provides the relationship between pressure, velocity and elevation along a streamline. P + ρV 2/2 + ρgz = constant along streamline The same relationship, but in a slightly different form, can be derived by applyingĬonservation of momentum to a fluid element along any streamline in the flow, giving
This relationship is a form of the Bernoulli's equation. If there is no pump or turbine in the system, then the equation becomes In many cases, the head loss (mainly due to viscous effects) can be ignored. In the Conservation of Energy section, it was shown that for a control volume, the energy equation can be simplified to In addition, the concept of energy and hydraulic grade A velocity measurement device called a Pitot tube willĪlso be presented. RestrictionsĪpplication of Bernoulli's equation are also clearly stated to avoid The details of the derivation are simplified, withĪttention focused on proper use of the equation. In this section, Bernoulli's equation willīe introduced.


 0 kommentar(er)
0 kommentar(er)
